Which of the following fractions has a decimal equivalent that is a terminating decimal?
A. 10/189
B. 15/196
C. 16/225
D. 25/144
E. 39/ 128
Answer: E
RULE: If denominator of a fraction has just the prime factors of 2 or 5 or both it is terminating otherwise not
128 = 2*2*2*2*2*2*2 => has only factors of 2..hence the ans
Tuesday, November 18, 2008
Problem Solving - 54
This year Henry will save a certain amount of his income, and he will spend the rest. Next year Henry will have no income, but for each dollar that he saves this year, he will have 1 + r dollars available to spend. In terms of r, what fraction of his income should Henry save this year so that next year the amount he was available to spend will be equal to half the amount that he spends this year?
(A) 1/(r+2)
(B) 1/2(r+2)
(C) 1/(3r+2)
(D) 1/(r+3)
(E) 1/(2r+3)
Answer: E
Let total income = x
Let saved = y
=> spent = x-y
Total dollars available that he can spend next year = y(1+r)
Given y(1+r) = (x-y)/2
=> y = x/(2r+3)
Fraction (y/x) = 1/(2r+3)
Hence E
(A) 1/(r+2)
(B) 1/2(r+2)
(C) 1/(3r+2)
(D) 1/(r+3)
(E) 1/(2r+3)
Answer: E
Let total income = x
Let saved = y
=> spent = x-y
Total dollars available that he can spend next year = y(1+r)
Given y(1+r) = (x-y)/2
=> y = x/(2r+3)
Fraction (y/x) = 1/(2r+3)
Hence E
Labels:
GMAT Prep,
Problem Solving,
Ratio,
Word problem
Saturday, November 08, 2008
Problem Solving - 53
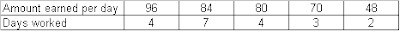 A student worked 20 days. For each of the amount shown (see attached table) in the first row of the table, second row gives the number of days the student earned that amount. Median amount of money earned per day for 20 days is?
A student worked 20 days. For each of the amount shown (see attached table) in the first row of the table, second row gives the number of days the student earned that amount. Median amount of money earned per day for 20 days is? A) 96
B) 84
C) 80
D) 70
E) 48
Answer: B
Median day = 20+1)/2 = 10.5 th -- money earned was 84
= Average value of 10th and 11th day in the sequence = Median amount of money
Average value of 10th day = 84
Average value of 11th day = 84
Average value of 10th and 11th day = 84 ans
Friday, November 07, 2008
Data Sufficiency - 50
What is the median number of employees assigned per project for the projects at Company Z?
(1) 25 percent of the projects at Company Z have 4 or more employees assigned to each project.
(2) 35 percent of the projects at Company Z have 2 or fewer employees assigned to each project.
Answer: OA - C
From Statement 1): It is given that 25 percent of the projects at Company Z have 4 or more employees assigned to each project - but we donot know the percentage of projects who have employees less than 4 or in other words we do not have any information about the rest 75% projects ---- hence insufficient
From Statement 2): It is given that 35 percent of the projects at Company Z have 2 or fewer employees assigned to each project - but we donot know the percentage of projects who have employees more than 2 or in other words we do not have any information about the rest 65% projects---- hence insufficient
Taking both the statements together:
25 percent of the projects at Company Z have employees 4 , 5, 6..
35 percent of the projects at Company Z have employees 2, 1, 0
=> 40% of projects have 3 employees = > median value is 3
(1-35)employees -- (36-75)employees -- (76-100)employees
2 or less than 2 ---------3, 3, 3, ------------ 4 or more than 4
(1) 25 percent of the projects at Company Z have 4 or more employees assigned to each project.
(2) 35 percent of the projects at Company Z have 2 or fewer employees assigned to each project.
Answer: OA - C
From Statement 1): It is given that 25 percent of the projects at Company Z have 4 or more employees assigned to each project - but we donot know the percentage of projects who have employees less than 4 or in other words we do not have any information about the rest 75% projects ---- hence insufficient
From Statement 2): It is given that 35 percent of the projects at Company Z have 2 or fewer employees assigned to each project - but we donot know the percentage of projects who have employees more than 2 or in other words we do not have any information about the rest 65% projects---- hence insufficient
Taking both the statements together:
25 percent of the projects at Company Z have employees 4 , 5, 6..
35 percent of the projects at Company Z have employees 2, 1, 0
=> 40% of projects have 3 employees = > median value is 3
(1-35)employees -- (36-75)employees -- (76-100)employees
2 or less than 2 ---------3, 3, 3, ------------ 4 or more than 4
Monday, November 03, 2008
Problem Solving - 52
A boat traveled up stream a distance of 90 miles at an average speed of (v-3) mph and then traveled the same distance downstream at an average speed of (v+3) mph. If the trip upstream took half an hour longer than the trip downstream, how many hours did it take the boat to travel downstream?
(A) 2.5
(B) 2.4
(C) 2.3
(D) 2.2
(E) 2.1
Answer: A
Total upstream time taken by boat to travel = 90/ (v-3) hrs
Total downstream time taken by boat to travel = 90/ (v+3) hrs
It is given that upstream took half an hour longer than the trip downstream:
=> 90/(v-3) - 90/(v+3) = 1/2
=> [90*(v+3) - 90(v-3)] / [(v^2) -9)] = 1/2
=> 90*[(v+3)-(v-3)] / [(v^2) -9] = 1/2
=> 90*6/ [(v^2) -9] = 1/2
=> v^2 - 9 = 2*90*6
=> v^2 = 2*90*6 + 9 = 2*9*10*6 + 9 = 9(2*10*6+1) = 9(121) = 9*11*11
=> v = 3*11 = 33
We are suppose to calculate = 90/(v+3) = 90/36 = 30/12 = 5/2 = 2.5 ans
(A) 2.5
(B) 2.4
(C) 2.3
(D) 2.2
(E) 2.1
Answer: A
Total upstream time taken by boat to travel = 90/ (v-3) hrs
Total downstream time taken by boat to travel = 90/ (v+3) hrs
It is given that upstream took half an hour longer than the trip downstream:
=> 90/(v-3) - 90/(v+3) = 1/2
=> [90*(v+3) - 90(v-3)] / [(v^2) -9)] = 1/2
=> 90*[(v+3)-(v-3)] / [(v^2) -9] = 1/2
=> 90*6/ [(v^2) -9] = 1/2
=> v^2 - 9 = 2*90*6
=> v^2 = 2*90*6 + 9 = 2*9*10*6 + 9 = 9(2*10*6+1) = 9(121) = 9*11*11
=> v = 3*11 = 33
We are suppose to calculate = 90/(v+3) = 90/36 = 30/12 = 5/2 = 2.5 ans
Labels:
GMAT Prep,
Problem Solving,
Speed Time and Distance
Problem Solving - 51
Each of the 10 machines works at the same constant rate of doing certain job. The amount of time needed by 10 machines, working together to complete the job is 16 hrs. How many hours are needed if only 8 machines working together were to complete the job?
A. 18
B. 20
C. 22
D. 24
E. 26
Answer: B
10 machines, working at same constant rate, take time to complete a job = 16 hrs
thus 1 machine takes time to complete a job = 10 * 16 = 160 hrs
=> 8 machines will take = 160/8 = 20 hrs to complete the job.
A. 18
B. 20
C. 22
D. 24
E. 26
Answer: B
10 machines, working at same constant rate, take time to complete a job = 16 hrs
thus 1 machine takes time to complete a job = 10 * 16 = 160 hrs
=> 8 machines will take = 160/8 = 20 hrs to complete the job.
Labels:
GMAT Prep,
Problem Solving,
Work and time
Subscribe to:
Posts (Atom)
