DS Question - 25

Is 5^k less than 1,000?

(1) 5^(k-1) is less than 3000
(2) 5^(k-1) = 5^k - 500

Answer: B

From statement (1) - It is given that 5^(k-1) less than 3000
=> 5^k/5 less than 3000
=> 5^k less than 15000
=> 5^k could be either more than 1,000 or less than 1,000.
Hence insufficient

From statement (2) - It is given that 5^(k-1) = 5^k - 500
=> 5^k/5 = (5^k) - 500
=> 5^k = 5*(5^k) - 2500
=> (5-1)*5^k = 2500
=> 4*5^k = 2500
=> 5^k = 2500/4 = 625

Hence 5^k less than 1,000.

Hence sufficient.

DS Question - 24

What is the 999th term of the series S ?

(1) The first 4 four terms of S are (1 + 1)² , (2 + 1)² , (3 + 1)² , and (4 + 1)².
(2) For every x, the xth term of S is (x + 1)².

Answer: B

From statement (1) - It is given that the 1st 4 four terms of S are (1 + 1)² , (2 + 1)² , (3 + 1)² , and (4 + 1)². We only know the first four terms. We cannot assume that terms following the first 4 terms will be like -- nth term = (n+1)^2.
There can be a sequence that follows a different rule for any term in it

From statement (2) - It is given that for every x, the xth term of S is (x + 1)². Hence sufficient as it implies "for any number x that refers to the term in S."

Problem Solving - 20

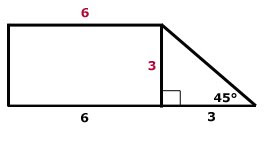What is the area of the trapezoid pictured to the right?

(A) 22.5

(B) 24

(C) 27

(D) 45

(E) 54


Answer: A

Since the triangle is a right isosceles triangle, the other side of the triangle (the height of the trapezoid) must also be 3. The top base if the trapezoid must be 6 since it is the opposite side of a rectangle.

The area of a trapezoid = 1/2 (sum of parallel sides) × (distance between the parallel sides)
= 1/2 (9 + 6) (3) = 22.5

The area can also be found here by breaking up the figure into a rectangle (area of 6 × 3 = 18) and a triangle (area of ½ × 3 × 3 = 4.5) and adding these two areas.

The correct answer is A.

Problem Solving - 19

How many 5 digit numbers can be created if the following terms apply: the leftmost digit is even, the second is odd, the third is a non even prime and the fourth and fifth are two random digits not used before in the number?

a) 2520
b) 3150
c) 3360
d) 6000
e) 7500


Answer: Given OA - A is incorrect ... ans is 2688 which is not an option in the choices...

When 2nd and 3rd digit gets repeated:

The first digit will be a non zero even (2, 4, 6, 8) = 4 ways
3rd digit is a non even prime = (3, 5, 7) = 3 ways
2nd digit is a REPEAT of that prime: 1 way
the fourth digit has not been used: 8 ways
the fifth digit has not been used: 7 ways

Hence 4*3*8*7 = 672 ways

Now, the non repeating case:

1st digit will be a non zero even (2, 4, 6, 8) = 4 ways
3rd digit (3, 5, 7) = 3 ways
2nd (no repeat and odd) = 4 ways
4th digit = 7
5th digit = 6

Hence 4*3*4*7*6 = 2016

Total number of ways = 2016 + 672 = 2688 ways


Note:
1). 1 is neither a prime nor a composite number.
2). 2 is the only even prime number.

DS Question - 23

If x is a positive integer, then how many factors does x have ?

(1) x is divisible by one more positive integer than 3^4 is.

(2) x is the product of three different prime numbers


Answer: D

From statement (1) - x has 5 factors 1, 3, 9, 27, 81. Adding one more factor from statement (1) makes total number of factors to be six.
Thus x has 6 factors.
Hence sufficient

From statement (2) - x = abc where a, b, c are prime numbers. Thus in all x has 8 factors - 1, a, b, c, ab, bc, ac, abc.
Thus x has 8 factors.
Hence sufficient


Note: Here each condition gives a different answer but still satifies the sufficient conditions.

Manhattan Challenge Problem of the week! - 09/04/07

Stephanie, Regine, and Brian ran a 20 mile race. Stephanie and Regine's combined times exceeded Brian's time by exactly 2 hours. If nobody ran faster than 8 miles per hour, who could have won the race?

I. Stephanie II. Regine III. Brian

(A) I only
(B) II only
(C) III only
(D) I or II only
(E) I, II, or III

Answer: D

Let the race time of Stephanie = S
Let the race time of Regine = R
Let the race time of Brian = B

It is given that -- Stephanie and Regine's combined times exceed Brian's time by 2 hours.

Hence S + R = B + 2 ------- (1)

To win the race, an individual's time must be less than 1/3 of the the combined times of all the runners.

Therefore for Brian to win the race (=> that Brian would have the lowest time) his time would need to be less than 1/3 of the combined times for all the runners.

=> B is less than 1/3 of (S+R+B)

=>3B<> is less than (S+R+B)

=> 2B is less than (S+R)

Making use of (1) in above

2B<> is less than (S+R)

=> 2B<> is less than B+2

=> B<2


Thus to win the race Brian's time must be less than 2 hours. which is impossible as fastest Brian run is 8 miles/hr => that the least amount of time in which he can complete the 20 mile race is 2.5 hrs.

Hence Stephanie and Regine as possible winners. Since the question gives us same information about Stephanie and Regine, we cannot state either one as a possible winner.

Hence, the correct answer is D

Manhattan Challenge Problem of the week! - 02/04/07

Triangle A has one side of length x. If (x^8) ^ 1/2 = 81 , what is the perimeter of Triangle A?

1) Triangle A has sides whose lengths are consecutive integers
2) Triangle A is NOT a right triangle

(A) Statement (1) alone is sufficient, but statement (2) alone is not sufficient.
(B) Statement (2) alone is sufficient, but statement (1) alone is not sufficient.
(C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.(D) Each statement ALONE is sufficient.
(E) Statements (1) and (2) TOGETHER are NOT sufficient.

Answer : C

OE - By simplifying the equation given in the question stem, we can solve for x as follows:

(x^8) ^ 1/2 = 81

x^4 = 81

x = 3

Thus, we know that one side of Triangle A has a length of 3.

Statement (1) tells us that Triangle A has sides whose lengths are consecutive integers. Given that one of the sides of Triangle A has a length of 3, this gives us the following possibilities: (1, 2, 3) OR (2, 3, 4) OR (3, 4, 5).

However, the first possibility is NOT a real triangle, since it does not meet the following condition, which is true for all triangles: The sum of the lengths of any two sides of a triangle must always be greater than the length of the third side. Since 1 + 2 is not greater than 3, it is impossible for a triangle to have side lengths of 1, 2 and 3.

Thus, Statement (1) leaves us with two possibilities. Either Triangle A has side lengths 2, 3, 4 and a perimeter of 9 OR Triangle A has side lengths 3, 4, 5 and a perimeter of 12. Since there are two possible answers, Statement (1) is not sufficient to answer the question.

Statement (2) tells us that Triangle A is NOT a right triangle. On its own, this is clearly not sufficient to answer the question, since there are many non-right triangles that can be constructed with a side of length 3.

Taking both statements together, we can determine the perimeter of Triangle A.

From Statement (1) we know that Triangle A must have side lengths of 2, 3, and 4 OR side lengths of 3, 4, and 5. Statement (2) tells us that Triangle A is not a right triangle; this eliminates the possibility that Triangle A has side lengths of 3, 4, and 5 since any triangle with these side lengths is a right triangle (this is one of the common Pythagorean triples). Thus, the only remaining possibility is that Triangle A has side lengths of 2, 3, and 4, which yields a perimeter of 9.

The correct answer is C: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.