A certain characteristic in a large population has a distribution that is symmetric about the mean m.If 68 percent of the distribution lies within one Standard Deviation d of the mean, what percent of the distribution is less than m+d?
A. 16%
B. 32%
C. 48%
D. 84%
E. 92%
Answer: D
In a normal bell curved distribution, 50% are below the mean and 50% are over it
If 68% are distributed within 1 S.D of the mean then this implies that 34% are 1 S.D above the mean and 34% are 1 S.D below the mean i.e 34% between m and m+d and 34% between m-d and m
The distribution is symmetric about m also => 32/2 = 16% between 0 and m-d and 16% m+d and above.
Hence total that is less than m+d = 100-16 = 84%
OR
Distribution is symmetric around mean => 68/2 = 34% =>(Mean-S.D, Mean) = (Mean, Mean+S.D] = 34% . Thus below Mean+S.D = 50+34 = 84%
NOTE: For a normal bell-curve distribution, the percentage is approx 34% between the mean and 1 S.D. the percentage is approximately 13.6% between 1 SD and 2 SD, the percentage is approximately 2% between 2 S.D and on...
Tuesday, December 18, 2007
Tuesday, November 27, 2007
Data Sufficiency - 33
Is |x - 1| less than 1 ?
1). (x - 1)^2 less than and equal to 1
2). x^2 - 1 greater than 0
Answer: E
|x-1| less than 1 is only true when 0 less than x less than 1
From statement (1): (x-1)^2<=1
True when 0<=x<=2
If x=0.5, then |x-1| less than 1 is true
If x=2, then |x-1| less than 1 is not true
Hence insufficient
From statement (2): x^2>1 means x>1 and x<-1
True when x=1.5, but not when x=3
Hence insufficient
Statement (1) and (2) together: 1 isless than x is less than and equal to 2
Taking x=1.5 and x=2
Hence insufficient
1). (x - 1)^2 less than and equal to 1
2). x^2 - 1 greater than 0
Answer: E
|x-1| less than 1 is only true when 0 less than x less than 1
From statement (1): (x-1)^2<=1
True when 0<=x<=2
If x=0.5, then |x-1| less than 1 is true
If x=2, then |x-1| less than 1 is not true
Hence insufficient
From statement (2): x^2>1 means x>1 and x<-1
True when x=1.5, but not when x=3
Hence insufficient
Statement (1) and (2) together: 1 is
Taking x=1.5 and x=2
Hence insufficient
Problem Solving - 30
Which of the following is always equal to sqrt (9 + x^2 - 6x)?
a) x - 3
b) 3 + x
c)|3 - x|
d)|3 + x|
e) 3 - x
Answer: C
sqrt (9+x^2-6x)
= sqrt( (3-x)^2 )
= |3-x|
a) x - 3
b) 3 + x
c)|3 - x|
d)|3 + x|
e) 3 - x
Answer: C
sqrt (9+x^2-6x)
= sqrt( (3-x)^2 )
= |3-x|
Data Sufficiency - 32
What is the value of x?
1) (-x)^3 = -x^3
2) (-x)^2 = -x^2
Answer: B
From statement (1):
if x = 0 both sides are equal
if x = 1 both sides are again equal {(-1)^3 = -1 & -1^3 = 1}
=> x = 0 or x = 1
Hence insufficient
From statement (2):
x can only be zero because the square of a number other than zero cannot be negative
{(-1)^2 = 1 which is not equal to -(1)^2)}
=> from above it is sufficient to say that x = 0
Hence sufficient
1) (-x)^3 = -x^3
2) (-x)^2 = -x^2
Answer: B
From statement (1):
if x = 0 both sides are equal
if x = 1 both sides are again equal {(-1)^3 = -1 & -1^3 = 1}
=> x = 0 or x = 1
Hence insufficient
From statement (2):
x can only be zero because the square of a number other than zero cannot be negative
{(-1)^2 = 1 which is not equal to -(1)^2)}
=> from above it is sufficient to say that x = 0
Hence sufficient
Monday, November 05, 2007
Data Sufficiency - 31
Is |x - 1| less than 1 ?
(1). (x - 1) ^2 less than and equal to 1
(2). (x^2) - 1 greater than 0
Answer: E
From statement (1): (x - 1) ^2 less than and equal to 1
Now this is true only if 0 is less than and equal to x and x is less than and equal to 2. (We know that (x - 1) ^2 less than 1 is only true when 0 is less than x and x is less than 2)
When we take x = 0.5, then |x-1| less than 1 is true
When we take x = 2, then |x-1| less than1 does not holds true
Hence insufficient
From statement (2): x^2 greater than 1 => x is less than -1 and x is greater than 1
When we take x = 1.5, then x^2 greater than 1 is true
When we take x = 3, then x^2 greater than 1 does not holds true
Hence insufficient
Taking both statements (1) and (2) together -- We have 1 is less than x and x is less than and equal to 2
When we take x = 1.5, then 1 is less than x and x is less than and equal to 2 is true
When we take x = 2, then 1 is less than x and x is less than and equal to 2 does not holds true Hence insufficient
(1). (x - 1) ^2 less than and equal to 1
(2). (x^2) - 1 greater than 0
Answer: E
From statement (1): (x - 1) ^2 less than and equal to 1
Now this is true only if 0 is less than and equal to x and x is less than and equal to 2. (We know that (x - 1) ^2 less than 1 is only true when 0 is less than x and x is less than 2)
When we take x = 0.5, then |x-1| less than 1 is true
When we take x = 2, then |x-1| less than1 does not holds true
Hence insufficient
From statement (2): x^2 greater than 1 => x is less than -1 and x is greater than 1
When we take x = 1.5, then x^2 greater than 1 is true
When we take x = 3, then x^2 greater than 1 does not holds true
Hence insufficient
Taking both statements (1) and (2) together -- We have 1 is less than x and x is less than and equal to 2
When we take x = 1.5, then 1 is less than x and x is less than and equal to 2 is true
When we take x = 2, then 1 is less than x and x is less than and equal to 2 does not holds true Hence insufficient
Tuesday, October 23, 2007
Statistics - Rules and Tips!
1. Mean Average = total of quantities / number of quantities
2. The median is the "middle" number in a group (when arranged in ascending or descending order) consisting of an odd number of numbers, and the average of the two middle numbers if there are an even number of numbers
3. For a set of consecutive integers, the median is the the average of the first and the last integer
4. Mode is the most frequently recurring number/numbers among the given set of numbers. It can be more than one
5. Range is the difference between the largest number and smallest number is a set
6. Calculation of Standard Deviation (SD):
8. SD does not change when the same constant is added or subtracted to all the members of the set
9. If mean = maximum value it means that all values are equal and SD is 0
10. A set of numbers with range of zero means that all of the numbers are the same, hence the dispersion of the numbers from its mean is zero
11. For data with approximately the same mean, the greater the spread, the greater the SD.
12. SD is the square root of the average of the sum of square of the variation from the mean
13. The more uneven members are dispersed around their arithmetic average, the more their SD
14. You only need to know the difference between values and total number of values to compute SD
15. If we know all the numbers of the list, there is a definite SD, regardless of what it is, we can compute it and get an answer – this is helpful for DS questions
16. If the range is 0, then the SD must also be 0, because there is no variance
17. The SD of any list is not dependent on the average, but on the deviation of the numbers from the average. So just by knowing that two lists having different averages doesn't say anything about their standard deviation - different averages can have the same SD
18. The sum of the deviations of the elements from the mean must be 0
19.Closer the more values to the MEAN, lower the SD
20. If Range or SD of a list is 0, then the list will contain all identical elements
21. Standard Deviation is also useful when comparing the spread of two separate data sets that have approximately the same mean. The data set with the smaller Standard Deviation has a narrower spread of measurements around the mean and therefore usually has comparatively fewer high or low values.
In general, the more widely spread the values are, the larger the Standard Deviation is.
22. If you multiply all terms by x then SD =x times old SD and mean = x times old mean
23. For comparing the SD for two sets any information about mean ,median,mode and range are insufficient unless you can determine the individual terms from the given data
24. Symmetric about the mean means that the shape of the distribution on the right and left side of the curve are mirror-images of each other
25. For a given set of consecutive even numbers.. mean = median
26. When you have a set of consecutive numbers (integers, evens, odds, multiples), the mean is equal to the median
27. Good links for Normal Distribution:
http://www-stat.stanford.edu/~naras/jsm/NormalDensity/NormalDensity.html
http://davidmlane.com/hyperstat/z_table.html
http://www.integratedlearning.net/gmat/sample.asp
2. The median is the "middle" number in a group (when arranged in ascending or descending order) consisting of an odd number of numbers, and the average of the two middle numbers if there are an even number of numbers
3. For a set of consecutive integers, the median is the the average of the first and the last integer
4. Mode is the most frequently recurring number/numbers among the given set of numbers. It can be more than one
5. Range is the difference between the largest number and smallest number is a set
6. Calculation of Standard Deviation (SD):
- Find the mean,
 , of the values.
, of the values. - For each value xi calculate its deviation (
 ) from the mean.
) from the mean. - Calculate the squares of these deviations.
- Find the mean of the squared deviations. This quantity is the variance σ2.
- Take the square root of the variance.
8. SD does not change when the same constant is added or subtracted to all the members of the set
9. If mean = maximum value it means that all values are equal and SD is 0
10. A set of numbers with range of zero means that all of the numbers are the same, hence the dispersion of the numbers from its mean is zero
11. For data with approximately the same mean, the greater the spread, the greater the SD.
12. SD is the square root of the average of the sum of square of the variation from the mean
13. The more uneven members are dispersed around their arithmetic average, the more their SD
14. You only need to know the difference between values and total number of values to compute SD
15. If we know all the numbers of the list, there is a definite SD, regardless of what it is, we can compute it and get an answer – this is helpful for DS questions
16. If the range is 0, then the SD must also be 0, because there is no variance
17. The SD of any list is not dependent on the average, but on the deviation of the numbers from the average. So just by knowing that two lists having different averages doesn't say anything about their standard deviation - different averages can have the same SD
18. The sum of the deviations of the elements from the mean must be 0
19.Closer the more values to the MEAN, lower the SD
20. If Range or SD of a list is 0, then the list will contain all identical elements
21. Standard Deviation is also useful when comparing the spread of two separate data sets that have approximately the same mean. The data set with the smaller Standard Deviation has a narrower spread of measurements around the mean and therefore usually has comparatively fewer high or low values.
In general, the more widely spread the values are, the larger the Standard Deviation is.
22. If you multiply all terms by x then SD =x times old SD and mean = x times old mean
23. For comparing the SD for two sets any information about mean ,median,mode and range are insufficient unless you can determine the individual terms from the given data
24. Symmetric about the mean means that the shape of the distribution on the right and left side of the curve are mirror-images of each other
25. For a given set of consecutive even numbers.. mean = median
26. When you have a set of consecutive numbers (integers, evens, odds, multiples), the mean is equal to the median
27. Good links for Normal Distribution:
http://www-stat.stanford.edu/~naras/jsm/NormalDensity/NormalDensity.html
http://davidmlane.com/hyperstat/z_table.html
http://www.integratedlearning.net/gmat/sample.asp
Wednesday, October 03, 2007
Problem Solving - 29
IF s is the product of integers from 100 to 200, inclusive, and t is the product of integers from 100 to 201, inclusive, what is 1/s + 1/t in terms of t?
A. (201) ^2 / t
B. [(202) (201)]/t
C. 201/t
D. 202/t
E. [(202) (201)]/(t^2)
Answer: D
Given s = 100 * ... * 200
Given t = 100 * ... * 200 * 201
=> s = t/201
Hence 1/s + 1/t = 201/t + 1/t = 202/t
A. (201) ^2 / t
B. [(202) (201)]/t
C. 201/t
D. 202/t
E. [(202) (201)]/(t^2)
Answer: D
Given s = 100 * ... * 200
Given t = 100 * ... * 200 * 201
=> s = t/201
Hence 1/s + 1/t = 201/t + 1/t = 202/t
Problem Solving - 28
According to the directions on a can of frozen orange juice concentrate, 1 can of concentrate is to be mixed with 3 cans of water to make orange juice. How many 12-ounce cans of the concentrate are required to prepare 200 6-ounce servings of orange juice?
A. 25
B. 34
C. 60
D. 67
E. 100
Answer: A
4 cans of orange juice need 1 can of concentrate.
200 cans 6-ounce of orange juice need 50 cans 6-ounce concentrate.
so 12-ounce concentrate = 50/2 = 25 cans
OR
Let number of 12 ounce cans required = x
number of 12 ounce cans of water required = 3x
Total required servings of Orange juice = 200*6 ounce
Hence
x(12) + 3x(12) = 200*6
48x= 200*6
x=25
Hence A
A. 25
B. 34
C. 60
D. 67
E. 100
Answer: A
4 cans of orange juice need 1 can of concentrate.
200 cans 6-ounce of orange juice need 50 cans 6-ounce concentrate.
so 12-ounce concentrate = 50/2 = 25 cans
OR
Let number of 12 ounce cans required = x
number of 12 ounce cans of water required = 3x
Total required servings of Orange juice = 200*6 ounce
Hence
x(12) + 3x(12) = 200*6
48x= 200*6
x=25
Hence A
Problem Solving - 27
Problem Solving - 26
n = 2*3*5*7*11*13/77k ...... If n is an integer and then which of the following could be the value of k?
(A) 22
(B) 26
(C) 35
(D) 54
(E) 60
Answer: B
n = 2*3*5*7*11*13/77k = 2*3*5*7*11*13/7*11*k = 2*3*5*13/k
=> k must be the product of any combination of product of these numbers.
From the given choices only 26 ------ (2*13) fits.
(A) 22
(B) 26
(C) 35
(D) 54
(E) 60
Answer: B
n = 2*3*5*7*11*13/77k = 2*3*5*7*11*13/7*11*k = 2*3*5*13/k
=> k must be the product of any combination of product of these numbers.
From the given choices only 26 ------ (2*13) fits.
Problem Solving - 25
Two canoe riders must be selected from each of two groups of campers. One group consists of three men and one woman, and the other group consists of two women and one man. What is the probability that two men and two women will be selected?
(A) 1/6
(B) 1/4
(C) 2/7
(D) 1/3
(E) 1/2
Answer: E
1st Group: 3 Men, 1 Woman
2nd Group: 1 Man, 2 Women
Total number of ways of selection: 4C2 * 3C2 = 18
No of ways of selecting two men and two women:
1. 2 men and 0 woman from 1st group and 0 men and 2 women from 2nd group = 3C2 = 3
2. 1 man and 1 woman from 1st group and 1 man and 1 woman from 2nd group = 3C1* 2C1 = 6 Thus Total ways from the above = 3 + 6 = 9
Therefore Probability = 9/18 = 1/2
(A) 1/6
(B) 1/4
(C) 2/7
(D) 1/3
(E) 1/2
Answer: E
1st Group: 3 Men, 1 Woman
2nd Group: 1 Man, 2 Women
Total number of ways of selection: 4C2 * 3C2 = 18
No of ways of selecting two men and two women:
1. 2 men and 0 woman from 1st group and 0 men and 2 women from 2nd group = 3C2 = 3
2. 1 man and 1 woman from 1st group and 1 man and 1 woman from 2nd group = 3C1* 2C1 = 6 Thus Total ways from the above = 3 + 6 = 9
Therefore Probability = 9/18 = 1/2
Saturday, June 30, 2007
DS Question - 30
If q is a multiple of prime numbers, is q a multiple of r?
1) r is less than 4
2) q = 18
Answer: E
From Statement (1) -- q can be positive and r can be negative.
r can also be a real number but not necessarily an integer.
Hence insufficient.
From Statement (2) -- q = 18.
But r can be negative or can be positive.
r can also be a real number not an integer
Hence insufficient
Taking both statements (1) and (2) together -- Again r can be positive or negative. And again r can also be a real number.
Hence insufficient
1) r is less than 4
2) q = 18
Answer: E
From Statement (1) -- q can be positive and r can be negative.
r can also be a real number but not necessarily an integer.
Hence insufficient.
From Statement (2) -- q = 18.
But r can be negative or can be positive.
r can also be a real number not an integer
Hence insufficient
Taking both statements (1) and (2) together -- Again r can be positive or negative. And again r can also be a real number.
Hence insufficient
Tuesday, June 26, 2007
DS Question - 29
If x and y are integers, does IxI = y ?
(1) (y^2 - x^2) = 0
(2) xy/(x+y) = 0
Answer: B
Statement (1) insufficient -- y can take any value i.e can be +ve or -ve. We cannot assume y to be +ve. Therefore y may or may not be equal to x
Statement (2) sufficient -- xy/(x+y) = 0 => xy = 0 => x = 0 or y = 0
In case x = 0, then y cannot be equal to 0. Hence y cannot be equal to x.
In case y = 0, then x cannot be equal to 0. Hence y cannot be equal to x.
Therefore sufficient.
Hence B
(1) (y^2 - x^2) = 0
(2) xy/(x+y) = 0
Answer: B
Statement (1) insufficient -- y can take any value i.e can be +ve or -ve. We cannot assume y to be +ve. Therefore y may or may not be equal to x
Statement (2) sufficient -- xy/(x+y) = 0 => xy = 0 => x = 0 or y = 0
In case x = 0, then y cannot be equal to 0. Hence y cannot be equal to x.
In case y = 0, then x cannot be equal to 0. Hence y cannot be equal to x.
Therefore sufficient.
Hence B
DS Question - 28
Is the three-digit number n less than 550?
1) The product of the digits in n is 30
2) The sum of the digits in n is 10
Answer: C
From statement (1) : the factors of 30 are 1,2,3,5,6,10,15,30
Now because the number must be digits (single number) we do not need to consider 10,15 and 50
Now if the hundreds digit of the 3-digit number = any digit among the 1,2,3 digits ---> answer to the question is clearly Yes.
But if the hundreds digit = 5 or 6 ---> answer to the question is No.
Hence (1) alone is insufficient.
From statement (2) : There are different combinations where the sum of digits can be equal to 10. e.g 541 and 145.
Hence (2) alone is insufficient.
Combining statements (1) and (2) we get :
If the hundreds digit= 5 , the second digit can only be 1,2,3 because if the digit is equal to 6 it violates statement (2) Hence in this case answer to the question is Yes.
If hundreds digit = 6 then the number n must contain 5 so as to satisfy the first statement but then it will violate statement (2) as the total of digits of n will exceed 10
Thus no 3-digit number exists with the hundreds digit equal to 6 satisfying both the statements together.
Hence the number n will always be less than 550 as it will be the combination of 1, 2, 3 and 5
Hence ans is C
1) The product of the digits in n is 30
2) The sum of the digits in n is 10
Answer: C
From statement (1) : the factors of 30 are 1,2,3,5,6,10,15,30
Now because the number must be digits (single number) we do not need to consider 10,15 and 50
Now if the hundreds digit of the 3-digit number = any digit among the 1,2,3 digits ---> answer to the question is clearly Yes.
But if the hundreds digit = 5 or 6 ---> answer to the question is No.
Hence (1) alone is insufficient.
From statement (2) : There are different combinations where the sum of digits can be equal to 10. e.g 541 and 145.
Hence (2) alone is insufficient.
Combining statements (1) and (2) we get :
If the hundreds digit= 5 , the second digit can only be 1,2,3 because if the digit is equal to 6 it violates statement (2) Hence in this case answer to the question is Yes.
If hundreds digit = 6 then the number n must contain 5 so as to satisfy the first statement but then it will violate statement (2) as the total of digits of n will exceed 10
Thus no 3-digit number exists with the hundreds digit equal to 6 satisfying both the statements together.
Hence the number n will always be less than 550 as it will be the combination of 1, 2, 3 and 5
Hence ans is C
Problem Solving - 24
On his drive to work, Bob listens to one of three radio stations, A,B, or C. He first turns to A. If A is playing a song he likes, he listens to it; if not, he turns to B. If B is playing a song he likes, he listens to it; if not, he turns to C. If C is playing a song he likes, he listens to it; if not, he turns off the radio. For each station , the probability is 0.30 that any given moment the station is playing a song Leo likes. On his drive to work, what is the probability that Bob will hear a song he likes?
A) 0.027
B) 0.090
C) 0.417
D) 0.657
E) 0.900
Answer: D
Probability Leo listens to A = (Probability that A is playing a song of Leo's choice ) = 0.3
Probability Leo listens to B = (Probability that A is not playing a song of Leo's choice ) * (Probability that B is playing a song of Leo's choice ) = (1-0.3) * 0.3 = 0.7*0.3
Probobility Leo listens to C = (Probability that A is not playing a song of Leo's choice ) * (Probability that B is not playing a song of Leo's choice ) * (Probability that C is playing a song of Leo's choice ) = 0.7 * 0.7 * 0.3
Total Probability = 0.3 + 0.7*0.3 + 0.7*0.7*0.3 = 0.657
A) 0.027
B) 0.090
C) 0.417
D) 0.657
E) 0.900
Answer: D
Probability Leo listens to A = (Probability that A is playing a song of Leo's choice ) = 0.3
Probability Leo listens to B = (Probability that A is not playing a song of Leo's choice ) * (Probability that B is playing a song of Leo's choice ) = (1-0.3) * 0.3 = 0.7*0.3
Probobility Leo listens to C = (Probability that A is not playing a song of Leo's choice ) * (Probability that B is not playing a song of Leo's choice ) * (Probability that C is playing a song of Leo's choice ) = 0.7 * 0.7 * 0.3
Total Probability = 0.3 + 0.7*0.3 + 0.7*0.7*0.3 = 0.657
Problem Solving - 23
If x is an integer divisible by 15 but not divisible by 20, then x CANNOT be divisible by which of the following?
(A) 6
(B) 10
(C) 12
(D) 30
(E) 150
Answer: C
x is divisible by 15 -> x is divisible by 3 and 5
x is not divisible by 20 -> x is not divisible by 4
Now because x is divisible by 15, it has 3 and 5 as factors and because x is not divisible by 20, it definitely does not have 4 as a factor .
In the given options only 12 is the number with 4 as a factor.
Thus x will not be divisible by 12. Hence C is the answer.
(A) 6
(B) 10
(C) 12
(D) 30
(E) 150
Answer: C
x is divisible by 15 -> x is divisible by 3 and 5
x is not divisible by 20 -> x is not divisible by 4
Now because x is divisible by 15, it has 3 and 5 as factors and because x is not divisible by 20, it definitely does not have 4 as a factor .
In the given options only 12 is the number with 4 as a factor.
Thus x will not be divisible by 12. Hence C is the answer.
Problem Solving - 22
A certain restaurant offers 6 kinds of cheese and 2 kinds of fruit for it dessert platter. If each dessert platter contains an equal number of kinds of cheese and kinds of fruit, how many different dessert platters could the restaurant offer?
(A) 8
(B) 12
(C) 15
(D) 21
(E) 27
Answer: E
There are two kinds of platter ---- 1 cheese + 1 fruit
Total types of platter -- 6 * 2= 12 ---(1)
For 2 cheese + 2 fruits
Total -- 6C2 * 2C2 = 15 * 1 = 15 ---(2)
Hence adding (1) and (2) we get total = 12 + 15 = 27
Friday, June 01, 2007
DS Question - 27
The area of a parallelogram is 100. What is the perimeter of the parallelogram ?
1) the base of the parallelogram is 10
2) one of the angles of the parallelogram is 45 degree
Answer: C
From (1) - For a parallelogram, Area = Base*Height => Height = 10 - There are infinite ways to draw a parallelogram with 100 as area, as long as the height is 10 units.( parallelograms with varying slants from 1 to 179 degrees) -- insufficent
From (2) - one of the angles is 45 degrees - hence the opposite angle is 45 degrees too, and the two remaining angles wil be 135 degrees each. But this doesn't tell us the measure of the sides to determine the perimeter - insufficient
From(1) and (2) together
From (2) we know that there is only one of such parallelograms that has an angle 45 to the base.
Base = 10. One angle = 45 degrees
In Parallelogram opposite angles are equal ..
Hence there are 2*45 degrees
Sum of all angles = 360
Thus 2*45 + 2 x = 360 which gives each other angle as 135 degrees
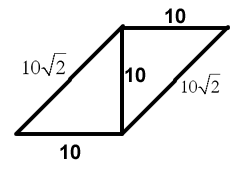
Note: If we are able to draw the figure on given DS question it implies conditions given are sufficient.
1) the base of the parallelogram is 10
2) one of the angles of the parallelogram is 45 degree
Answer: C
From (1) - For a parallelogram, Area = Base*Height => Height = 10 - There are infinite ways to draw a parallelogram with 100 as area, as long as the height is 10 units.( parallelograms with varying slants from 1 to 179 degrees) -- insufficent
From (2) - one of the angles is 45 degrees - hence the opposite angle is 45 degrees too, and the two remaining angles wil be 135 degrees each. But this doesn't tell us the measure of the sides to determine the perimeter - insufficient
From(1) and (2) together
From (2) we know that there is only one of such parallelograms that has an angle 45 to the base.
Base = 10. One angle = 45 degrees
In Parallelogram opposite angles are equal ..
Hence there are 2*45 degrees
Sum of all angles = 360
Thus 2*45 + 2 x = 360 which gives each other angle as 135 degrees

Note: If we are able to draw the figure on given DS question it implies conditions given are sufficient.
Manhattan Challenge Problem of the week! - 05/28/07
Baseball's World Series matches 2 teams against each other in a best-of-seven series. The first team to win four games wins the series and no subsequent games are played. If you have no special information about either of the teams, what is the probability that the World Series will consist of fewer than 7 games?
(A) 12.5%
(B) 25%
(C) 31.25%
(D) 68.75%
(E) 75%
Answer: D
OE - In order to determine the probability that the World Series will last fewer than 7 games, we can first determine the probability that the World Series WILL last exactly 7 games and then subtract this value from 1.
In order for the World Series to last exactly 7 games, the first 6 games of the series must results in 3 wins and 3 losses for each team.
Let's analyze one way this could happen:
Game 1 -----Game 2 -----Game 3 -----Game 4 -----Game 5 -----Game 6
T1 Wins-----T1 Wins-----T1 Wins-----T1 Loses-----T1 Loses-----T1 Loses
There are many other ways this could happen. Using the permutation formula, there are 6!/(3!)(3!) = 20 ways for the two teams to split the first 6 games (3 wins for each).
There are then 2 possible outcomes to break the tie in Game 7. Thus, there are a total of 20 × 2 = 40 ways for the World Series to last the full 7 games.
The probability that any one of these 40 ways occurs can be calculated from the fact that the probability of a team winning a game equals the probability of a team losing a game = 1/2.
Given that 7 distinct events must happen in any 7 game series, and that each of these events has a probability of 1/2, the probability that any one particular 7 game series occurs is
(1/2) ^ 7 = 1/ 128
Since there are 40 possible different 7 game series, the probability that the World Series will last exactly 7 games is:
40 * 1/128 = 40/ 128 = .3125 = 31.255%
Thus the probability that the World Series will last fewer than 7 games is:
100% - 31.25% = 68.75%.
The correct answer is D.
(A) 12.5%
(B) 25%
(C) 31.25%
(D) 68.75%
(E) 75%
Answer: D
OE - In order to determine the probability that the World Series will last fewer than 7 games, we can first determine the probability that the World Series WILL last exactly 7 games and then subtract this value from 1.
In order for the World Series to last exactly 7 games, the first 6 games of the series must results in 3 wins and 3 losses for each team.
Let's analyze one way this could happen:
Game 1 -----Game 2 -----Game 3 -----Game 4 -----Game 5 -----Game 6
T1 Wins-----T1 Wins-----T1 Wins-----T1 Loses-----T1 Loses-----T1 Loses
There are many other ways this could happen. Using the permutation formula, there are 6!/(3!)(3!) = 20 ways for the two teams to split the first 6 games (3 wins for each).
There are then 2 possible outcomes to break the tie in Game 7. Thus, there are a total of 20 × 2 = 40 ways for the World Series to last the full 7 games.
The probability that any one of these 40 ways occurs can be calculated from the fact that the probability of a team winning a game equals the probability of a team losing a game = 1/2.
Given that 7 distinct events must happen in any 7 game series, and that each of these events has a probability of 1/2, the probability that any one particular 7 game series occurs is
(1/2) ^ 7 = 1/ 128
Since there are 40 possible different 7 game series, the probability that the World Series will last exactly 7 games is:
40 * 1/128 = 40/ 128 = .3125 = 31.255%
Thus the probability that the World Series will last fewer than 7 games is:
100% - 31.25% = 68.75%.
The correct answer is D.
Manhattan Challenge Problem of the week! - 05/21/07
Edwin is planning to drive from Boston to New Orleans. By what percent would his travel time be reduced if Edwin decides to split the driving time equally with his friend George, instead of making the trip alone?
(1) The driving distance from Boston to New Orleans is 1500 miles.
(2) George’s driving speed is 1.5 times Edwin’s driving speed.
Answer: B
OE - The question asks for the percent decrease in Edwin’s travel time. To determine this, we need to be able to find the ratio between, T1 (the travel time if Edwin drives alone) and T2 (the travel time if Edwin and George drive together). Note that we do NOT need to determine specific values for T1 and T2; we only need to find the ratio between them.
Percentage change is defined as follows: Difference/Original = (T1 - T2)/ T1 = 1 - (T2/ T1)
Ultimately, we can solve the percentage change equation above by simply determining the value of T2 /T1
Using the formula Rate × Time = Distance, we can write equations for each of the 2 possible trips
T1 = Travel time if Edwin drives alone
T2 = Travel time if Edwin and George drive together
E = Edwin’s Rate
G = George’s Rate
D = Distance of the trip
If Edwin travels alone: ET1 = D
If Edwin and George travel together: .5(E + G)T2 = D
(Since Edwin and George split the driving equally, the rate for the trip is equal to the average of Edwin and George’s individual rates).
Since both trips cover the same distance (D), we can combine the 2 equations as follows:
ET1 = .5(E + G)T2
Then, we can isolate the ratio of the times (T2/T1) as follows:
E/ .5(E + G) = T2/ T1
Now we look at the statements to see if they can help us to solve for the ratio of the times.
Statement (1) gives us a value for D, the distance, which does not help us since D is not a variable in the ratio equation above.
Statement (2) tells us that George’s rate is 1.5 times Edwin’s rate. Thus, G = 1.5E. We can substitute this information into the ratio equation above:
E/ .5(E + G) = T2/ T1 ---> E/ .5(E + 1.5E) = T2/ T1 ---> E/ .5E + .75E = T2/T1
---> E/ 1.25E = T2/ T1 ---> 1/ 1.25 = T2/ T1 ---> .8 = T2/ T1
Thus, using this ratio we can see that Edwin’s travel time for the trip will be reduced as follows:
1 - (T2/T1) = 1 - .8 = .2 ---> 20%
Statement (2) alone is sufficient to answer the question.
The correct answer is B.
(1) The driving distance from Boston to New Orleans is 1500 miles.
(2) George’s driving speed is 1.5 times Edwin’s driving speed.
Answer: B
OE - The question asks for the percent decrease in Edwin’s travel time. To determine this, we need to be able to find the ratio between, T1 (the travel time if Edwin drives alone) and T2 (the travel time if Edwin and George drive together). Note that we do NOT need to determine specific values for T1 and T2; we only need to find the ratio between them.
Percentage change is defined as follows: Difference/Original = (T1 - T2)/ T1 = 1 - (T2/ T1)
Ultimately, we can solve the percentage change equation above by simply determining the value of T2 /T1
Using the formula Rate × Time = Distance, we can write equations for each of the 2 possible trips
T1 = Travel time if Edwin drives alone
T2 = Travel time if Edwin and George drive together
E = Edwin’s Rate
G = George’s Rate
D = Distance of the trip
If Edwin travels alone: ET1 = D
If Edwin and George travel together: .5(E + G)T2 = D
(Since Edwin and George split the driving equally, the rate for the trip is equal to the average of Edwin and George’s individual rates).
Since both trips cover the same distance (D), we can combine the 2 equations as follows:
ET1 = .5(E + G)T2
Then, we can isolate the ratio of the times (T2/T1) as follows:
E/ .5(E + G) = T2/ T1
Now we look at the statements to see if they can help us to solve for the ratio of the times.
Statement (1) gives us a value for D, the distance, which does not help us since D is not a variable in the ratio equation above.
Statement (2) tells us that George’s rate is 1.5 times Edwin’s rate. Thus, G = 1.5E. We can substitute this information into the ratio equation above:
E/ .5(E + G) = T2/ T1 ---> E/ .5(E + 1.5E) = T2/ T1 ---> E/ .5E + .75E = T2/T1
---> E/ 1.25E = T2/ T1 ---> 1/ 1.25 = T2/ T1 ---> .8 = T2/ T1
Thus, using this ratio we can see that Edwin’s travel time for the trip will be reduced as follows:
1 - (T2/T1) = 1 - .8 = .2 ---> 20%
Statement (2) alone is sufficient to answer the question.
The correct answer is B.
Manhattan Challenge Problem of the week! - 04/30/07
How many terminating zeroes does 200! have?
(A) 40
(B) 48
(C) 49
(D) 55
(E) 64
Answer : C
OE - To determine how many terminating zeroes a number has, we need to determine how many times the number can be divided evenly by 10. (For example, the number 404000 can be divided evenly by 10 three times, as follows:
404000/10 = 40400
40400/10 = 4040
4040/10 = 404
We can see that the number has three terminating zeroes because it is divisible by 10 three times.) Thus, to arrive at an answer, we need to count the factors of 10 in 200! Recall that
200! = 200 * 199 * 198 ........... * 4 * 3 * 2 * 1
Each factor of 10 consists of one prime factor of 2 and one prime factor of 5. Let’s start by counting the factors of 5 in 200!. Starting from 1, we get factors of 5 at 5, 10, 15, . . . , 190, 195, and 200, or every 5th number from 1 to 200. Thus, there are 200/5 or 40 numbers divisible by five from 1 to 200. Therefore, there are at least 40 factors of 5 in 200!.
We cannot stop counting here, because some of those multiples of 5 contribute more than just one factor of 5. Specifically, any multiple of 52 (or 25) and any multiple of 53 (or 125) contribute additional factors of 5. There are 8 multiples of 25 (namely, 25, 50, 75, 100, 125, 150, 175, 200). Each of these 8 numbers contributes one additional factor of 5 (in addition to the one we already counted) so we now have counted 40 + 8, or 48 factors of 5. Finally, 125 contributes a third additional factor of 5, so we now have 48 + 1 or 49 total factors of 5 in 200!.
Let us now examine the factors of 2 in 200!. Since every even number contributes at least one factor of 2, there are at least 100 factors of 2 in 200! (2, 4, 6, 8 . . .etc). Since we are only interested in the factors of 10 — a factor of 2 paired with a factor of 5 — and there are more factors of 2 than there are of 5, the number of factors of 10 is constrained by the number of factors of 5. Since there are only 49 factors of 5, each with an available factor of 2 to pair with, there are exactly 49 factors of 10 in 200!.
It follows that 200! has 49 terminating zeroes, and the correct answer is C.
(A) 40
(B) 48
(C) 49
(D) 55
(E) 64
Answer : C
OE - To determine how many terminating zeroes a number has, we need to determine how many times the number can be divided evenly by 10. (For example, the number 404000 can be divided evenly by 10 three times, as follows:
404000/10 = 40400
40400/10 = 4040
4040/10 = 404
We can see that the number has three terminating zeroes because it is divisible by 10 three times.) Thus, to arrive at an answer, we need to count the factors of 10 in 200! Recall that
200! = 200 * 199 * 198 ........... * 4 * 3 * 2 * 1
Each factor of 10 consists of one prime factor of 2 and one prime factor of 5. Let’s start by counting the factors of 5 in 200!. Starting from 1, we get factors of 5 at 5, 10, 15, . . . , 190, 195, and 200, or every 5th number from 1 to 200. Thus, there are 200/5 or 40 numbers divisible by five from 1 to 200. Therefore, there are at least 40 factors of 5 in 200!.
We cannot stop counting here, because some of those multiples of 5 contribute more than just one factor of 5. Specifically, any multiple of 52 (or 25) and any multiple of 53 (or 125) contribute additional factors of 5. There are 8 multiples of 25 (namely, 25, 50, 75, 100, 125, 150, 175, 200). Each of these 8 numbers contributes one additional factor of 5 (in addition to the one we already counted) so we now have counted 40 + 8, or 48 factors of 5. Finally, 125 contributes a third additional factor of 5, so we now have 48 + 1 or 49 total factors of 5 in 200!.
Let us now examine the factors of 2 in 200!. Since every even number contributes at least one factor of 2, there are at least 100 factors of 2 in 200! (2, 4, 6, 8 . . .etc). Since we are only interested in the factors of 10 — a factor of 2 paired with a factor of 5 — and there are more factors of 2 than there are of 5, the number of factors of 10 is constrained by the number of factors of 5. Since there are only 49 factors of 5, each with an available factor of 2 to pair with, there are exactly 49 factors of 10 in 200!.
It follows that 200! has 49 terminating zeroes, and the correct answer is C.
Thursday, May 31, 2007
Manhattan Challenge Problem of the week! - 04/23/07
Which of the following sets includes ALL of the solutions of x that will satisfy the equation:
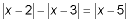
Answer: OA - C
For the second interval 2 less than x less than 3, we can solve the equation by rewriting the expression inside the first absolute value sign as positive and by rewriting the expressions inside the other absolute values signs as negative:
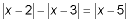
Answer: OA - C
OE - One way to solve equations with absolute values is to solve for x over a series of intervals. In each interval of x, the sign of the expressions within each pair of absolute value indicators does not change.
In the equation Ix-2I - Ix-3I = Ix-5I , there are 4 intervals of interest:
x less than 2 - In this interval, the value inside each of the three absolute value expressions is negative.
2 less than x less than 3 - In this interval, the value inside the first absolute value expression is positive, while the value inside the other two absolute value expressions is negative.
3 less than x less than 5 - In this interval, the value inside the first two absolute value expressions is positive, while the value inside the last absolute value expression is negative.
5 less than x - In this interval, the value inside each of the three absolute value expressions is positive.
Use each interval for x to rewrite the equation so that it can be evaluated without absolute value signs.
For the first interval, x less than 2, we can solve the equation by rewriting each of the expressions inside the absolute value signs as negative (and thereby remove the absolute value signs):
- x + 2 - ( -x + 3 ) = - x + 5
- x + 2 + x - 3 = - x + 5
x = 6
Notice that the solution x = 6 is NOT a valid solution since it lies outside the interval x less than 2. (Remember, we are solving the equation for x SUCH THAT x is within the interval of interest).
For the second interval 2 less than x less than 3, we can solve the equation by rewriting the expression inside the first absolute value sign as positive and by rewriting the expressions inside the other absolute values signs as negative:
x - 2 - ( -x + 3 ) = - x + 5
x - 2 + x - 3 = - x + 5
3x = 10
x = 10/3
Notice, again, that the solution x = 10/3 is NOT a valid solution since it lies outside the interval 2 less than x less than 3
For the third interval 3 less than x less than 5, we can solve the equation by rewriting the expressions inside the first two absolute value signs as positive and by rewriting the expression inside the last absolute value sign as negative:
x - 2 - ( x - 3 ) = - x + 5
x - 2 - x + 3 = - x + 5
x = 4
The solution x = 4 is a valid solution since it lies within the interval 3 less than x less than 5
Finally, for the fourth interval 5 less than x, we can solve the equation by rewriting each of the expressions inside the absolute value signs as positive:
x - 2 - ( x - 3 ) = x - 5
x - 2 - x + 3 = x - 5
x = 6
The solution x = 6 is a valid solution since it lies within the interval 5 less than x.
We conclude that the only two solutions of the original equation are x = 4 and x = 6. Only answer choice C contains all of the solutions, both 4 and 6, as part of its set.
Therefore, C is the correct answer.
Manhattan Challenge Problem of the week! - 16/04/07
x and y are positive integers. 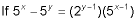 , what is the value of xy?
, what is the value of xy?
(A) 48
(B) 36
(C) 24
(D) 18
(E) 12
Answer: OA - E
5^x - 5^y = 2^(y-1) * 5^(x-1)
Divide both sides by 5^(x-1)....we get
[5^x/ 5^(x-1)] - [5^y/ 5^(x-1)] = 2^(y-1)
Simplifying the first tem we get
5 - [5^x/ 5^(x-1)] = 2^(y-1)
Add [5^y/ 5^(x-1)] to both sides...we get
5 = 2^(y-1) + [5^y/ 5^(x-1)]
We know that 2^(y-1) and [5^y/ 5^(x-1)] are positive and each of them is less than 5
We can now list all the possibilities, by testing small integer values for y. We only have to test a few values because we know that 2^(y-1) must be less than 5, which means that y can only be 1, 2 or 3. (If y is 4, then 2^(y-1) would be 8, which is greater than 5.)
If y = 1, then 2^(y-1) = 2^(1-1) = 2^0 , which means that [5^y/ 5^(x-1)] must equal 4 (remember, the sum of the two terms must be equal to 5). However, since x and y are positive integers, there is no way to make [5^y/ 5^(x-1)] equal to 4.
If y = 2, then 2^(y-1) = 2^(2-1) = 2^1 = 2, which means that [5^y/ 5^(x-1)] must equal 3. However, since x and y are positive integers, there is no way to make [5^y/ 5^(x-1)] equal to 3.
If y = 3, then 2^(y-1) = 2^(3-1) = 2^2 = 4 , which means that cmust equal 1. This is possible. Using y = 3, we can solve for x as follows:
[5^y/ 5^(x-1)] = 1
=> [5^3/ 5^(x-1)] = 1
=> 5^3 = 5^(x-1)
=> 3 = x-1
=> x = 4
The only possible solution is y = 3 and x = 4. Therefore, xy = (4)(3) = 12. The correct answer is E.
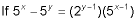 , what is the value of xy?
, what is the value of xy? (A) 48
(B) 36
(C) 24
(D) 18
(E) 12
Answer: OA - E
5^x - 5^y = 2^(y-1) * 5^(x-1)
Divide both sides by 5^(x-1)....we get
[5^x/ 5^(x-1)] - [5^y/ 5^(x-1)] = 2^(y-1)
Simplifying the first tem we get
5 - [5^x/ 5^(x-1)] = 2^(y-1)
Add [5^y/ 5^(x-1)] to both sides...we get
5 = 2^(y-1) + [5^y/ 5^(x-1)]
We know that 2^(y-1) and [5^y/ 5^(x-1)] are positive and each of them is less than 5
We can now list all the possibilities, by testing small integer values for y. We only have to test a few values because we know that 2^(y-1) must be less than 5, which means that y can only be 1, 2 or 3. (If y is 4, then 2^(y-1) would be 8, which is greater than 5.)
If y = 1, then 2^(y-1) = 2^(1-1) = 2^0 , which means that [5^y/ 5^(x-1)] must equal 4 (remember, the sum of the two terms must be equal to 5). However, since x and y are positive integers, there is no way to make [5^y/ 5^(x-1)] equal to 4.
If y = 2, then 2^(y-1) = 2^(2-1) = 2^1 = 2, which means that [5^y/ 5^(x-1)] must equal 3. However, since x and y are positive integers, there is no way to make [5^y/ 5^(x-1)] equal to 3.
If y = 3, then 2^(y-1) = 2^(3-1) = 2^2 = 4 , which means that cmust equal 1. This is possible. Using y = 3, we can solve for x as follows:
[5^y/ 5^(x-1)] = 1
=> [5^3/ 5^(x-1)] = 1
=> 5^3 = 5^(x-1)
=> 3 = x-1
=> x = 4
The only possible solution is y = 3 and x = 4. Therefore, xy = (4)(3) = 12. The correct answer is E.
Thursday, May 03, 2007
Problem Solving - 21
Mrs. Napueta has been given film vouchers. Each voucher allows the holder to see a film without charge. She decides to distribute them among her four nephews so that each nephew gets at least two vouchers. How many vouchers has Mrs. Napueta been given if there are 120 ways that she could distribute the vouchers?
(A) 13
(B) 14
(C) 15
(D) 16
(E) more than 16
Answer: C
Formula - Number of ways of distributing n identical things among r persons when each person may get any number of things = C(n+r-1, r-1)
Hence
Let total number of vouchers = n
All 4 nephews get atleast 2 vouchers, thus remaining vouchers to be distributed among 4 nephews where each can get 0 or more vouchers = n-8
Using the formula above we get = C(n-8+4-1, 3) = (n-8+4-1)C3 = 120 = (n-5)(n-6)(n-7) = 120 * 3! = 720
Hence n = 15
(A) 13
(B) 14
(C) 15
(D) 16
(E) more than 16
Answer: C
Formula - Number of ways of distributing n identical things among r persons when each person may get any number of things = C(n+r-1, r-1)
Hence
Let total number of vouchers = n
All 4 nephews get atleast 2 vouchers, thus remaining vouchers to be distributed among 4 nephews where each can get 0 or more vouchers = n-8
Using the formula above we get = C(n-8+4-1, 3) = (n-8+4-1)C3 = 120 = (n-5)(n-6)(n-7) = 120 * 3! = 720
Hence n = 15
Tuesday, May 01, 2007
DS Question - 26
Is 5^k less than 1,000?
(1) 5^(k-1) greater than 3,000
(2) 5^(k-1) = 5^k - 500
Answer: D
From statement (1) - 5^(k-1) is greater than 3000
=> 5^k/5 is greater than 3000
=> 5^k is greater than 15000
Hence sufficient
From statement (2) - 5^(k-1) = 5^k - 500
=> 5^(k-1) = 5^k - 500
=> 5^k - 5^(k-1) = 500
=> 5^k(1- 5^-1) = 500
=> 5^k(4/5) = 500
=> 5^k = 2500/4 = 625
Therefore 5^k is less than 1000
Hence sufficient
(1) 5^(k-1) greater than 3,000
(2) 5^(k-1) = 5^k - 500
Answer: D
From statement (1) - 5^(k-1) is greater than 3000
=> 5^k/5 is greater than 3000
=> 5^k is greater than 15000
Hence sufficient
From statement (2) - 5^(k-1) = 5^k - 500
=> 5^(k-1) = 5^k - 500
=> 5^k - 5^(k-1) = 500
=> 5^k(1- 5^-1) = 500
=> 5^k(4/5) = 500
=> 5^k = 2500/4 = 625
Therefore 5^k is less than 1000
Hence sufficient
Saturday, April 28, 2007
DS Question - 25
Is 5^k less than 1,000?
(1) 5^(k-1) is less than 3000
(2) 5^(k-1) = 5^k - 500
Answer: B
From statement (1) - It is given that 5^(k-1) less than 3000
=> 5^k/5 less than 3000
=> 5^k less than 15000
=> 5^k could be either more than 1,000 or less than 1,000.
Hence insufficient
From statement (2) - It is given that 5^(k-1) = 5^k - 500
=> 5^k/5 = (5^k) - 500
=> 5^k = 5*(5^k) - 2500
=> (5-1)*5^k = 2500
=> 4*5^k = 2500
=> 5^k = 2500/4 = 625
Hence 5^k less than 1,000.
Hence sufficient.
(1) 5^(k-1) is less than 3000
(2) 5^(k-1) = 5^k - 500
Answer: B
From statement (1) - It is given that 5^(k-1) less than 3000
=> 5^k/5 less than 3000
=> 5^k less than 15000
=> 5^k could be either more than 1,000 or less than 1,000.
Hence insufficient
From statement (2) - It is given that 5^(k-1) = 5^k - 500
=> 5^k/5 = (5^k) - 500
=> 5^k = 5*(5^k) - 2500
=> (5-1)*5^k = 2500
=> 4*5^k = 2500
=> 5^k = 2500/4 = 625
Hence 5^k less than 1,000.
Hence sufficient.
Subscribe to:
Posts (Atom)